Amortized Variational Inference in Hierarhical Distributions
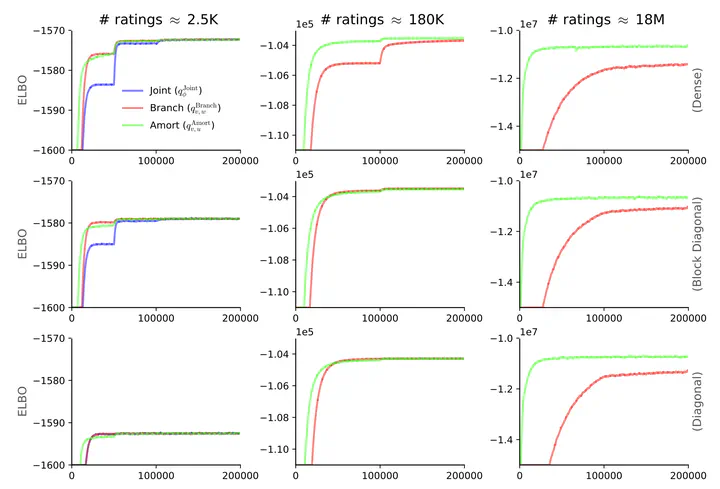 We show that amortized VI is more accurate, fast, and scalable than other methods
We show that amortized VI is more accurate, fast, and scalable than other methodsAbstract
It is difficult to use subsampling with variational inference in hierarchical models since the number of local latent variables scales with the dataset. Thus, inference in hierarchical models remains a challenge at large scale. It is helpful to use a variational family with a structure matching the posterior, but optimization is still slow due to the huge number of local distributions. Instead, this paper suggests an amortized approach where shared parameters simultaneously represent all local distributions, and a “feature pooling” network is learned to represent conditionally i.i.d. observations. This approach is similarly accurate as using a given joint distribution (e.g. a full-rank Gaussian) but is feasible on datasets that are several orders of magnitude larger. It is also dramatically faster than using a structured variational distribution.
Type
Publication
In Neural Information Processing Systems